DDPM: Denoising Diffusion Probabilistic Models
📅 최초 작성: 2025년 7월 13일
🔄 최종 업데이트: 2025년 08월 24일 18:12 (KST)
✨ 최근 변경사항: 전체 포스트 말투 통일(친근한 반말), 설명 흐름 개선, 직관적 해석과 수학적 엄밀성의 균형 조정, 섹션 간 자연스러운 연결 추가
Jonathan Ho · Ajay Jain · Pieter Abbeel
Denoising Diffusion Probabilistic Models, NeurIPS 2020
arXiv 2006.11239 • GitHub Repository
📝 Abstract
확산 확률 모델(Diffusion Probabilistic Models, DDPM)은 데이터에 점차적으로 노이즈를 더한 후, 이를 다시 제거하는 과정을 학습해서 이미지를 만들어내는 모델이다. 쉽게 말하면, 이미지를 서서히 망가뜨린 뒤(노이즈 추가), 거꾸로 망가진 이미지를 고치는 법(노이즈 제거)을 배우는 방식이다.
이 접근법은 어려운 생성 문제를 “단계별 작은 노이즈 제거 문제”로 나누어 해결한다. 저자들은 CIFAR-10과 LSUN 데이터셋에서 높은 품질의 이미지를 만들어내며, GAN에서 자주 생기던 학습 불안정이나 모드 붕괴 같은 문제를 피할 수 있음을 보였다. 오늘날 Stable Diffusion, Midjourney 같은 이미지 생성 모델의 핵심 기반이 되었다.
여러 복잡한 개념들이 등장한다. 하나씩 차근차근 알아보자.
Langevin Dynamics: 물 분자들이 꽃가루를 무작위로 충돌시킴 (노이즈) -> 중력이나 점성이 특정 방향으로 끌어당김 (복원력) 와 같이 노이즈 이후에 복원 하는 동역학. DDPM에서는 가우시안 노이즈를 추가하고 학습된 방향성을 따라 점진적으로 원본 이미지를 복원하는 방식으로 활용
📝 Introduction
GAN과 VAE 같은 기존 생성 모델들은 뛰어난 성과를 냈지만, 각각 치명적인 단점이 있었다. GAN은 훈련이 불안정하고 모드 붕괴가 생기며, VAE는 만들어내는 이미지가 상대적으로 흐릿하다.
DDPM은 새로운 관점을 제안한다. 데이터를 점차적으로 “흐리게 만들고” 다시 “또렷하게 만드는 법”을 학습시키는 것이다. 이런 접근은 수학적으로는 변분 추론과 연결되고, 실험적으로는 고품질 이미지를 안정적으로 생성하는 데 성공했다.
아래는 DDPM이 실제로 생성한 샘플 이미지이다.

또한, DDPM의 핵심 구조는 아래와 같이 Forward/Reverse Process의 마르코프 체인으로 시각화할 수 있습니다.
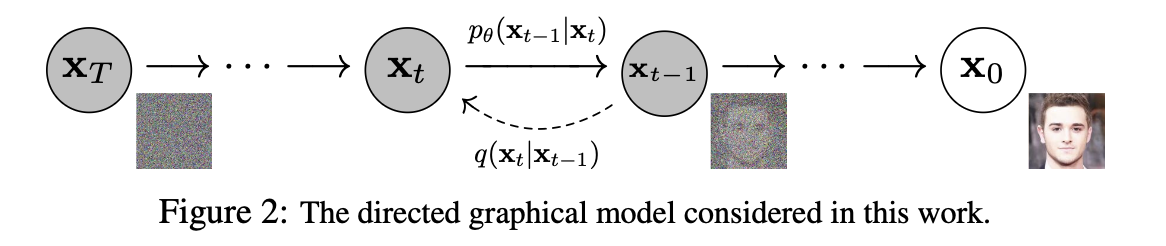
이 글에서는 DDPM의 핵심 아이디어와 동작 원리를 수식과 함께 차근차근 알아보고, 실제로 어떻게 이미지를 생성하는지 단계별로 살펴보자.
마찬가지로 여러 개념들이 등장한다. Diffusion models learn distributions generated by complex Langevin dynamics 논문에 기반한 내용으로, 배경 지식이 어느 정도 필요하다. 하나씩 차근차근 알아보자.
Background
DDPM은 크게 두 단계로 나눌 수 있다.
- 순방향 과정 (Forward Process): 원본 데이터에 점차적으로 노이즈를 추가 → 결국 완전한 노이즈 상태에 도달
- 역방향 과정 (Reverse Process): 완전한 노이즈에서 출발 → 점차 노이즈를 제거해 원본 같은 데이터를 복원
이 두 과정은 마르코프 체인(Markov Chain) 구조를 따른다. 즉, 현재 상태는 오직 직전 상태에만 의존한다. 복잡한 과정을 단순한 연쇄 구조로 바꾸어 다루기 쉽게 만든 것이다.
마르코프 체인(Markov Chain)
Markov Property: 현재 상태 $x_t$는 바로 직전 상태 $x_{t-1}$에만 의존한다. 그 이전의 모든 과거는 무시된다.

- 0차 마르코프: 모든 상태가 독립
- 1차 마르코프: 현재 상태는 직전 상태에만 의존 ← DDPM이 사용하는 구조
- 2차 이상: 현재 상태가 여러 개의 과거 상태에 의존
DDPM은 각 노이즈 레벨을 하나의 상태로 보고, 순방향/역방향 모두 1차 마르코프 체인으로 정의한다. 이 단순한 구조 덕분에 긴 과정을 수학적으로 쉽게 다룰 수 있다.
각 논문에 나오는 수식들을 차근차근 이해하자.
Forward Process
\[q(x_{1:T}|x_0) = \prod_{t=1}^T q(x_t|x_{t-1}), \quad q(x_t|x_{t-1}) = \mathcal{N}(x_t;\,\sqrt{1-\beta_t}\,x_{t-1},\,\beta_t I) \tag{1}\]Forward process 는 이미지에 가우시안 노이즈를 추가하는 과정이다. 원본 이미지 $x_0$에서 시작해, 단계마다 가우시안 노이즈를 조금씩 섞는다. 이 과정을 $T$번 반복하면, 결국 무작위 노이즈 $x_T$가 된다.

왼쪽 항은 원본 이미지 $x_0$에서 시작해 최종적으로 순수한 노이즈 $x_T$에 도달하기까지의 전체 확률 과정을 의미한다. 즉, $x_0 \to x_1 \to \cdots \to x_T$로 이어지는 일련의 마르코프 체인 전체를 한 번에 기술한 표현이다. 여기서 $x_t$는 시점 $t$에서의 데이터(노이즈가 조금씩 추가된 이미지)를, $T$는 전체 단계 수를, $q$는 이 순방향 과정의 분포를 나타낸다
오른쪽 항은 이 긴 과정 중에서 한 단계 전이(transition)만을 나타낸다. 여기서는 직전 상태 $x_{t-1}$에서 새로운 상태 $x_t$로 넘어가는 규칙이 가우시안 분포로 주어져 있다. 구체적으로, 이전 샘플 $x_{t-1}$의 신호를 $\sqrt{1-\beta_t}$만큼 유지하고, 분산이 $\beta_t$인 가우시안 노이즈를 추가하여 $x_t$를 얻는다. 즉, 매 단계는 “직전 이미지에 약간의 흐림(노이즈)을 더하는 과정”이라고 이해할 수 있다
즉, $x_{t-1}$을 $\sqrt{1-\beta_t}$만큼 줄이고, 분산이 $\beta_t$인 가우시안 노이즈를 더한 값이 $x_t$가 된다.
\[x_t = \sqrt{1-\beta_t}\,x_{t-1} + \sqrt{\beta_t}\,\epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0,I)\]📋 변수 설명:
| 변수 | 의미 | 설명 |
|---|---|---|
| $q$ | 순방향 분포 | 고정된, 학습되지 않는 분포 |
| $p$ | 역방향 분포 | 학습 가능한 분포 |
| $x_0$ | 원본 데이터 | 완전한 이미지 |
| $x_t$ | 시점 t 데이터 | 노이즈가 추가된 이미지 |
| $T$ | 확산 단계 수 | 일반적으로 1000 |
| $\beta_t$ | 분산 스케줄 | 노이즈 추가 정도 제어 |
| $I$ | 단위 행렬 | 각 픽셀에 독립적 노이즈 |
| $\epsilon$ | 가우시안 노이즈 | $\sim \mathcal{N}(0, I)$ |
Reverse Process
\[p_\theta(x_{0:T}) = p(x_T) \prod_{t=1}^T p_\theta(x_{t-1}|x_t), \quad p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1};\,\mu_\theta(x_t, t),\,\Sigma_\theta(x_t, t)) \tag{2}\]Reverse process 는 Forward process의 반대 방향으로, 순수한 노이즈 $x_T$에서 시작해 원본 이미지 $x_0$을 복원하는 과정이다. 즉, 주어진 노이즈를 단계별로 조금씩 “덜 노이즈하게” 만들어가며 결국 실제 데이터와 유사한 이미지를 생성한다.
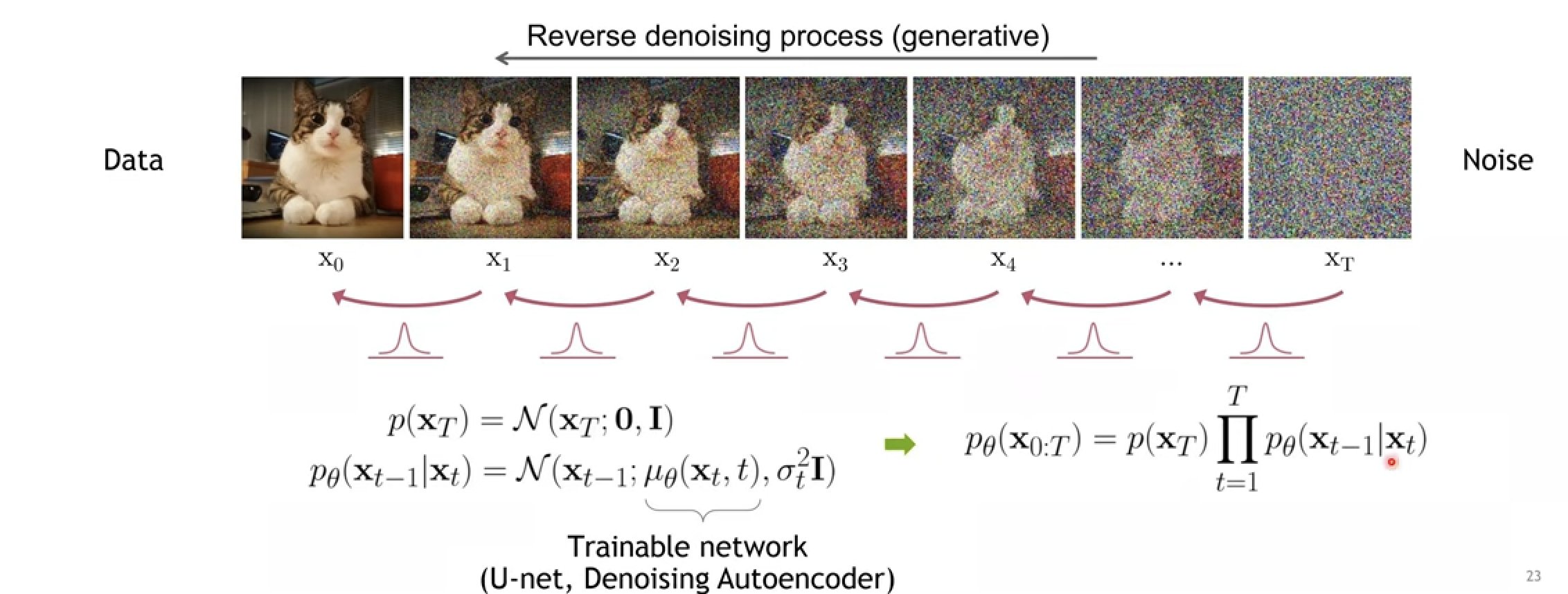
왼쪽 항은 $x_T \to x_{T-1} \to \cdots \to x_0$로 이어지는 전체 역방향 마르코프 체인을 나타낸다. 즉, 완전히 랜덤한 노이즈 분포 $p(x_T)$에서 시작해, 각 단계의 조건부 분포를 반복적으로 적용하여 최종적으로 원본 데이터 $x_0$에 도달하는 전체 과정을 한 번에 표현한 것이다. 여기서 $\theta$는 신경망이 학습을 통해 최적화하는 매개변수다.
오른쪽 항은 이 긴 복원 과정 중에서 한 단계 전이(transition)만을 나타낸다. Forward process에서는 노이즈를 더하는 규칙이 고정된 가우시안 분포였던 반면, Reverse process에서는 가우시안의 평균 $\mu_\theta(x_t,t)$를 신경망이 직접 예측한다. 이는 “현재 상태 $x_t$에서 더 깨끗한 상태 $x_{t-1}$로 어떻게 이동할 것인지”를 결정하는 역할을 한다. 공분산 $\Sigma_\theta(x_t,t)$는 보통 고정하거나 단순한 형태로 설정한다
여기서 시작점 $p(x_T)$는 표준 정규분포 $\mathcal{N}(0,I)$다. 즉, 완전한 랜덤 노이즈에서 시작한다. 각 단계의 평균 $\mu_\theta(x_t, t)$는 신경망이 예측한다. 이 값은 “노이즈를 얼마만큼 제거해야 하는지”를 알려주는 방향 신호다. 공분산 $\Sigma_\theta(x_t, t)$는 보통 고정하거나 단순한 형태를 사용한다.
📋 변수 설명:
| 변수 | 의미 | 설명 |
|---|---|---|
| $p_\theta$ | 역방향 분포 | 학습 가능한 분포 (매개변수 $\theta$) |
| $\theta$ | 신경망 매개변수 | U-Net 구조의 모든 가중치 |
| $x_{0:T}$ | 전체 변수 집합 | $(x_0, x_1, \ldots, x_T)$ |
| $p_{\theta}(x_{t-1} \mid x_t)$ | 역방향 전이 확률 | 이전 상태 예측 |
| $\mu_{\theta}(x_t, t)$ | 예측 평균 | 신경망이 예측하는 평균 |
| $\Sigma_{\theta}(x_t, t)$ | 예측 공분산 | 보통 고정값 사용 |
| $p(x_T)$ | 초기 노이즈 분포 | 표준 정규분포 |
Loss function
Loss는 모델이 원본 데이터 $x_0$를 얼마나 잘 설명하는지를 나타낸다. 우리가 직접적으로 구하고 싶은 것은 데이터 우도(likelihood) $\;p_\theta(x_0)\;$의 음의 로그값, 즉 $-\log p_\theta(x_0)$이다.
여기서 $p_\theta(x_{0:T})$는 전체 변수 $(x_0, x_1, \ldots, x_T)$에 대한 결합 확률 분포이며, 원하는 주변확률 $p_\theta(x_0)$를 얻으려면 나머지 $x_{1:T}$를 적분으로 소거해야 한다. 이를 위해 보조 분포를 도입해 수식을 변형한다:
\[\log p_\theta(x_0) = \log \int q(x_{1:T}|x_0)\; \frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}\, dx_{1:T}.\]분자와 분모에 보조 분포를 곱해준 뒤 기대값의 정의 $\;\mathbb{E}_q[f(X)] = \int f(X)\,q(X)\,dX\;$ 를 적용하면,
\[\log p_\theta(x_0) = \log\, \mathbb{E}_{q}\!\Bigg[\frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}\Bigg].\]이제 적분이 사라지고, 보조 분포 $q$에 대한 기대값 표현으로 바뀌었다. 이 단계가 중요하다: 바로 여기서부터 Jensen’s inequality를 적용해 변분 경계(ELBO)를 얻을 수 있다. Jensen의 부등식은 $\;\log \mathbb{E}[Z] \;\geq\; \mathbb{E}[\log Z]\;$를 보장한다. 이를 적용하면
\[\log p_\theta(x_0) \;\geq\; \mathbb{E}_{q}\!\Bigg[\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}\Bigg]. \tag{ELBO}\]즉, $\log p_\theta(x_0)$를 직접 계산할 수 없으니, 우리는 대신 하한(ELBO, Evidence Lower Bound)을 최대화하는 방식으로 학습을 진행한다.
이제 이를 Loss로 바꾸면:
\[L := \mathbb{E}[-\log p_\theta(x_0)] \;\leq\; \mathbb{E}_q\left[-\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}\right].\]여기서 Forward Process 의 (1) 식과 Reverse Process 의 (2) 식을 각각 전개하면:
-
Forward: \(q(x_{1:T}|x_0) = \prod_{t=1}^T q(x_t|x_{t-1})\)
-
Reverse: \(p_\theta(x_{0:T}) = p(x_T)\prod_{t=1}^T p_\theta(x_{t-1}|x_t)\)
이를 대입하면 Loss는 다음과 같이 정리된다:
\[\frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} = \frac{p(x_T)\prod_{t=1}^{T} p_\theta(x_{t-1}\mid x_t)} {\prod_{t=1}^{T} q(x_t\mid x_{t-1})} = p(x_T)\prod_{t=1}^{T} \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})}.\]로그를 취하면 곱이 합으로 바뀌기 때문에
\[-\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} = -\log p(x_T) -\sum_{t=1}^{T}\log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})}.\]따라서 최종 Loss는,
\[L = \mathbb{E}_q\left[-\log p(x_T) - \sum_{t=1}^T \log \frac{p_\theta(x_{t-1}|x_t)}{q(x_t|x_{t-1})}\right]. \tag{3}\]Loss function 분해
\[L = \underbrace{D_{KL}(q(x_T|x_0) \parallel p(x_T))}_{L_T} + \sum_{t>1} \underbrace{D_{KL}(q(x_{t-1}|x_t, x_0) \parallel p_\theta(x_{t-1}|x_t))}_{L_{t-1}} - \underbrace{\log p_\theta(x_0|x_1)}_{L_0} \tag{3}\]식 (3)을 $L_T, L_{t-1}, L_0$로 분해하는 이유는 원래의 복잡한 변분 경계 손실을 해석 가능한 구성 요소로 나누어 각각의 역할을 명확히 하기 위함이다. 즉, $L_T$는 최종 노이즈 분포가 표준 정규분포와 얼마나 가까운지 측정하는 Regularization on encoder, $\sum_{t>1} L_{t-1}$은 각 시점에서 모델이 올바르게 디노이징을 수행하는지를 평가하는 Denoising process, $L_0$는 최종적으로 원본 데이터를 잘 복원하는지를 확인하는 Recontruction on decoder으로 이해된다. 이러한 분해를 통해 하나의 거대한 최적화 문제를 작은 부분 문제로 나누어 학습을 안정화할 수 있고, 동시에 VAE의 ELBO와 구조적으로 대응되어 DDPM을 “다단계 확장된 VAE”로 해석할 수 있게 된다.
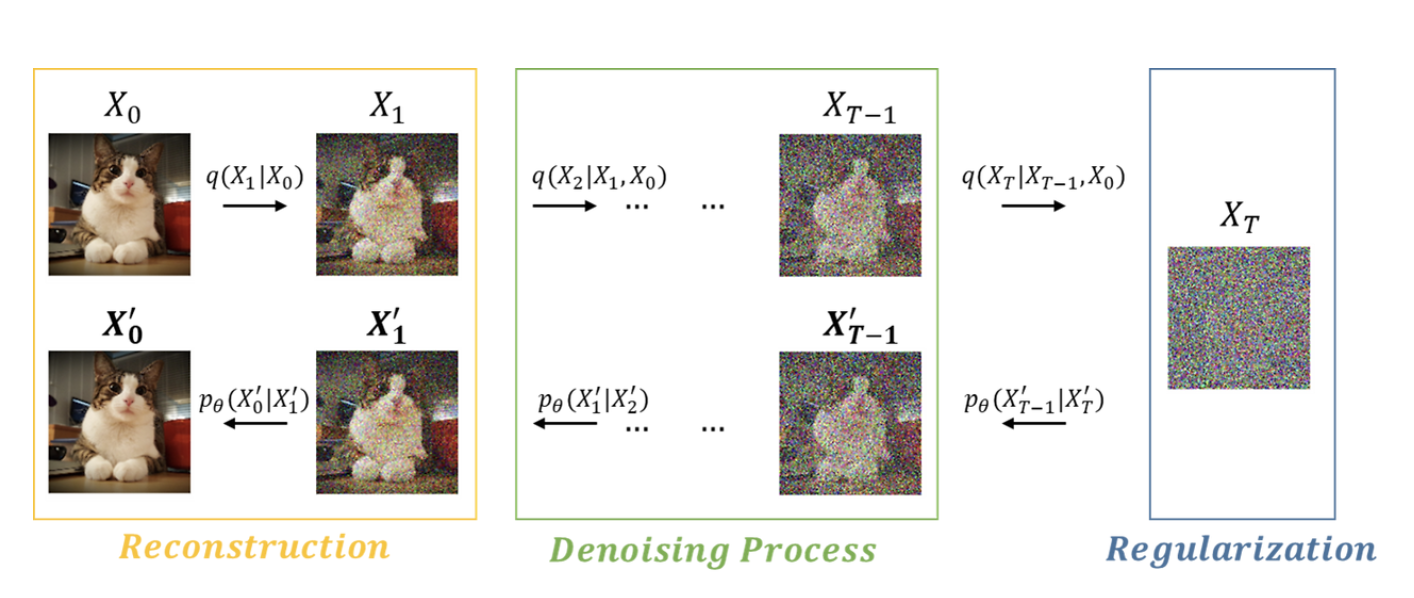
증명
출발점은 식 (3):
\[L = \mathbb{E}_q\!\left[-\log p(x_T) -\sum_{t=1}^{T}\log\frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})}\right]. \tag{3}\]베이즈 항등식으로 \(q(x_t\mid x_{t-1})\)를 posterior 형태로 바꾸면
\[q(x_t\mid x_{t-1}) = \frac{q(x_{t-1}\mid x_t,x_0)\,q(x_t\mid x_0)}{q(x_{t-1}\mid x_0)}.\]따라서 로그 비는 두 항으로 분해된다:
\[\log\frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})} = \log\frac{p_\theta(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t,x_0)} + \log\frac{q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)}.\]두 번째 합은 망원급수(telecope)로 정리되어
\[\sum_{t=1}^{T}\log\frac{q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)} = -\log q(x_T\mid x_0).\]이를 식 (3)에 대입 및 KL divergence 정의 $D_{\mathrm{KL}}(q(z)\,|\,p(z)) = \mathbb{E}_{q(z)}!\left[\log \frac{q(z)}{p(z)}\right].$ 를 이용하면
\[\begin{aligned} L &= \mathbb{E}_q\!\left[ -\log p(x_T) + \log q(x_T\mid x_0) -\sum_{t=1}^{T}\log\frac{p_\theta(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t,x_0)} \right] \\[2pt] &= \underbrace{\mathbb{E}_q\!\big[\log \tfrac{q(x_T\mid x_0)}{p(x_T)}\big]}_{D_{\mathrm{KL}}(q(x_T\mid x_0)\,\|\,p(x_T))} + \sum_{t=1}^{T} \underbrace{\mathbb{E}_q\!\big[\log \tfrac{q(x_{t-1}\mid x_t,x_0)}{p_\theta(x_{t-1}\mid x_t)}\big]}_{D_{\mathrm{KL}}(q(x_{t-1}\mid x_t,x_0)\,\|\,p_\theta(x_{t-1}\mid x_t))}. \end{aligned}\]즉,
\[{ L = D_{\mathrm{KL}}\!\big(q(x_T\mid x_0)\,\|\,p(x_T)\big) + \sum_{t=1}^{T} D_{\mathrm{KL}}\!\big(q(x_{t-1}\mid x_t,x_0)\,\|\,p_\theta(x_{t-1}\mid x_t)\big) } \tag{5}\]여기서 $t=1$ 항을 따로 떼어 $\,L_0$로 표기하면 ($q(x_0\mid x_1,x_0)=\delta(x_0)\Rightarrow D_{\mathrm{KL}}=!-\log p_\theta(x_0\mid x_1)$):
\[L_0 := -\log p_\theta(x_0\mid x_1).\]최종적으로
\[\boxed{ L = \underbrace{D_{\mathrm{KL}}(q(x_T\mid x_0)\,\|\,p(x_T))}_{L_T} + \sum_{t=2}^{T} \underbrace{D_{\mathrm{KL}}(q(x_{t-1}\mid x_t,x_0)\,\|\,p_\theta(x_{t-1}\mid x_t))}_{L_{t-1}} \;-\; \underbrace{\log p_\theta(x_0\mid x_1)}_{L_0} }\]의미 요약
- $L_T$: 최종 노이즈 $x_T$가 $p(x_T)=\mathcal{N}(0,I)$와 얼마나 가까운지 (보통 상수 취급).
- $\sum_{t=2}^{T} L_{t-1}$: 각 단계 디노이징이 올바른지 평가하는 핵심 학습 항.
- $L_0$: 마지막 재구성 우도(원본 복원 품질).
Forward process and $L_T$
\[\underbrace{D_{KL}(q(x_T|x_0)\,\|\,p(x_T))}_{L_T}\]Forward process의 분산 $\beta_t$는 이론적으로 학습 가능하지만, 저자들은 이를 고정된 상수로 두었다. 따라서 Forward process 에서는 학습 가능한 매개변수가 없으므로 이로 인해 $L_T$는 훈련 중 상수 취급한다.
Reverse process and $L_{1:T-1}$
\[\sum_{t>1} \underbrace{D_{KL}(q(x_{t-1}|x_t,x_0)\,\|\,p_\theta(x_{t-1}|x_t))}_{L_{t-1}}\]Reverse process 를 다시 살펴보면:
\[p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1};\,\mu_\theta(x_t,t),\,\Sigma_\theta(x_t,t)).\]🔧 공분산 $\Sigma_\theta$
- 학습하지 않고 $\Sigma_\theta(x_t,t) = \sigma_t^2 I$로 고정
- $\sigma_t^2$는 보통 $\beta_t$ 또는 $\tilde\beta_t = \frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t$
- 두 방식 모두 실험적으로 큰 차이가 없음
🔧 평균 $\mu_\theta$
Loss 전개에 따르면:
\[L_{t-1} = \mathbb{E}_q\!\left[\frac{1}{2\sigma_t^2}\|\tilde\mu_t(x_t,x_0) - \mu_\theta(x_t,t)\|^2\right] + C\]여기서 $\tilde\mu_t$는 Forward posterior 평균, $C$는 상수.
즉, 기본 접근은 $\mu_\theta$가 $\tilde\mu_t$를 직접 예측하는 것이다.
🔄 노이즈 $\epsilon$ 예측 방식
Forward 과정을 재매개변수화하면:
\[x_t = \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t}\,\epsilon, \quad \epsilon \sim \mathcal{N}(0,I).\]이를 활용해 평균 대신 노이즈 $\epsilon$을 예측하도록 바꾼다:
\[\mu_\theta(x_t,t) = \frac{1}{\sqrt{\alpha_t}}\Big(x_t - \frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\,\epsilon_\theta(x_t,t)\Big).\]이때 Loss는:
\[\mathbb{E}_{x_0,\epsilon}\!\left[\frac{\beta_t^2}{2\sigma_t^2 \alpha_t(1-\bar\alpha_t)} \|\epsilon - \epsilon_\theta(x_t,t)\|^2\right]\]꼴로 단순화된다 → 이는 여러 노이즈 레벨에서의 denoising score matching 구조.
📌 정리: 평균 예측 대신 노이즈 $\epsilon$ 예측이 더 직관적이고 효과적이며, Langevin dynamics와 유사한 해석을 제공한다.
3.3 Final reconstruction and $L_0$
\[\underbrace{\log p_\theta(x_0|x_1)}_{L_0}\]마지막 항은:
\[L_0 = -\log p_\theta(x_0|x_1),\]즉, 최종 단계에서 원본 데이터를 얼마나 잘 복원하는지를 나타낸다.
- VAE의 재구성 손실(reconstruction loss)과 대응
- 여러 단계를 거친 후 최종 출력이 원본과 얼마나 일치하는지 측정
- 샘플 품질과 직접적으로 연결되는 항
3.4 Weighted Variational Bound
앞의 분해식은 여전히 복잡하므로, 저자들은 가중치가 붙은 단순 MSE Loss로 변형한다.
최종 단순화된 목표는:
\[L_\text{simple} = \mathbb{E}_{t, x_0, \epsilon}\!\left[w_t \cdot \|\epsilon - \epsilon_\theta(x_t, t)\|^2 \right],\]여기서
- $x_t = \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t}\,\epsilon,\; \epsilon \sim \mathcal{N}(0,I)$
- $w_t = \tfrac{\beta_t^2}{2\sigma_t^2 \alpha_t (1-\bar\alpha_t)}$는 시점별 가중치
📌 정리:
- 복잡한 KL 항들의 합 → MSE 형태 Loss로 단순화
- 학습이 안정적이고 구현이 쉬움
- 이 손실은 곧 denoising score matching과 동일한 구조
- DDPM 학습은 결국 “노이즈 예측 MSE”를 최소화하는 문제로 귀결된다
Leave a comment